AVL树和红黑树

2016-10-31

技术分享会旨在：抛砖引玉，促进程序之间互相交流，培养公司内部良好的技术氛围。

1. Base

此次分享会默认大家清楚了解以下知识点：

二叉查找树(binary search tree)的定义和实现
AVL树的定义和实现
基础的C/C++知识

此次分享会主要和大家分享探讨以下内容

AVL树和红黑树的异同
树的旋转
红黑树的在STL中的应用(SGI STL)
红黑树在跳跃表中的应用

2. AVL树和红黑树的性质

###AVL树

高度为h的AVL树最少有S(h) = S(h-1) + S(h-2) + 1个节点
- $$S(h) = \frac{1}{\sqrt{5}}((\frac{1+\sqrt{5}}{2})^{h+2} - (\frac{1-\sqrt{5}}{2})^{h+2}) - 1$$
- $$\because \frac{(\frac{1-\sqrt{5}}{2})^{h+2}}{\sqrt(5)} < 1 \therefore S(h) > \frac{(\frac{1+\sqrt{5}}{2})^{h+2}}{\sqrt(5)} - 1$$
AVL树的高度不超过$$\frac{3}{2}log_2^N$$
查找时间复杂度: $$O(log_2^N)$$
插入时间复杂度: $$O(log_2^N)$$+0-2次旋转
删除时间复杂度: $$O(log_2^N)$$+若干次旋转

删除操作最多会造成$$O(log_2^N)$$次旋转，这种情况发生在删除最简AVL树的一个节点时发生。

###红黑树

红黑树的高度不超过$$2log_2^N$$
查找时间复杂度: $$O(log_2^N)$$
插入时间复杂度: $$O(log_2^N)$$+0-2次旋转
删除时间复杂度: $$O(log_2^N)$$+0-3次旋转

所有的AVL树都能不经旋转涂成红黑树，反之不行。

###红黑树和AVL树对比
结论：红黑树和AVL树时间复杂度是一样的，但是红黑树的统计性能更高！

以下是对它们处理百万随机数的性能统计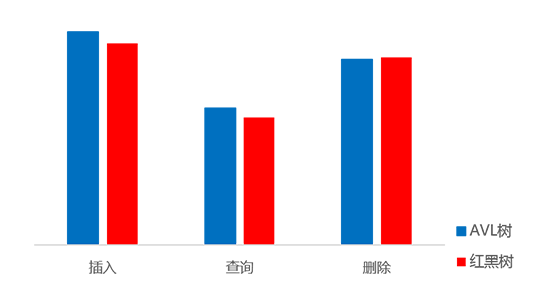

##3. 红黑树的插入和删除

插入

我参考的是SGI STL版本的红黑数实现，源码如下：

__rb_tree_rebalance(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
    //参数1为新增节点
    x->color == __rb_tree_red; //新增节点必须为红色
    while(x != root && x->parent->color == __rb__tree_red)
    {
        if(x->parent == x->parent->parent->left)
        {
            //父节点为组父节点的左节点
            __rb_tree_node_base* y = x->parent->parent->right; //令y为伯父节点
            if(y && y->color == __rb_tree_red)
            {
                //情况1
                //伯父节点存在并且为红色
                x->parent->color = __rb_tree_black;
                y->color = __rb_tree_black;
                x->parent->parent->color = __rb_tree_red;
                x = x->parent->parent; //上滤
            }
            else
            {
                //无伯父节点，或伯父节点为黑
                if(x == x->parent->right)
                {
                    //情况2
                    x = x->parent;
                    __rb_tree_rotate_left(x, root);
                }
                //情况3
                x->parent->color = __rb_tree_black;
                x->parent->parent->color = __rb_tree_red;
                __rb_tree_rotate_right(x->parent->parent, root);
            }
        }
        else
        {
            __rb_tree_node_base* y = x->parent->parent->left; //令y为伯父节点
            if(y && y->color == __rb_tree_red)
            {
                //情况4
                //伯父节点存在并且为红色
                x->parent->color = __rb_tree_black;
                y->color = __rb_tree_black;
                y->parent->parent->color = __rb_tree_red;
                x = x->parent->parent; //上滤
            }
            else
            {
                //无伯父节点，或伯父节点为黑
                if(x == x->parent->left)
                {
                    //情况5
                    x = x->parent;
                    __rb_tree_rotate_right(x, root);
                }
                //情况6
                x->parent->color = __rb_tree_black;
                x->parent->parent->color = __rb_tree_red;
                __rb_tree_left(x->parent->parent, root);
            }
        }
    }
    root->color = __rb_tree_black;
}

####左旋转动画
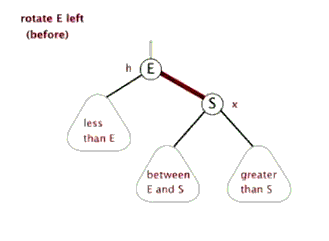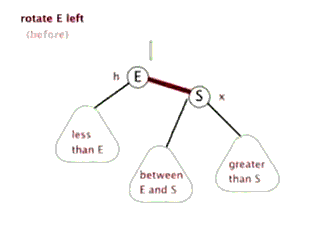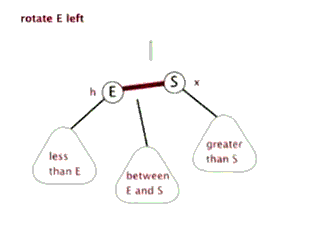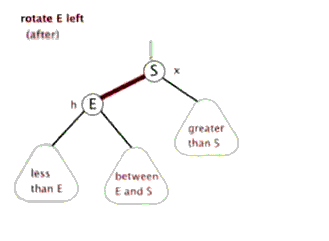
####右旋转动画
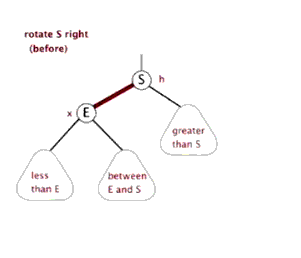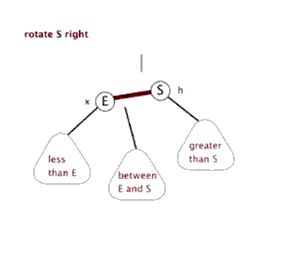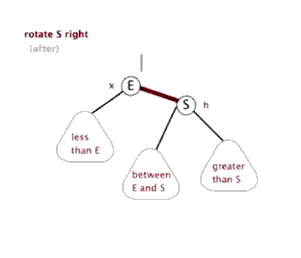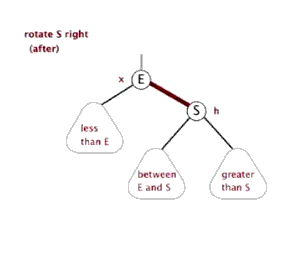
####情况1

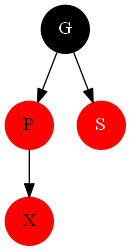
直接把父节点和伯父节点改成黑色，祖父节点改成红色，继续上滤就可以了。

####情况2

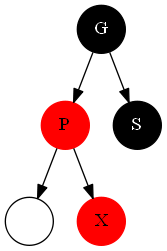
把子节点丰富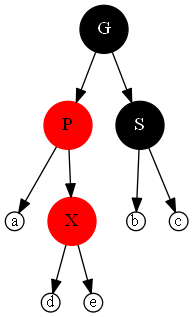

先对XP做一次左旋转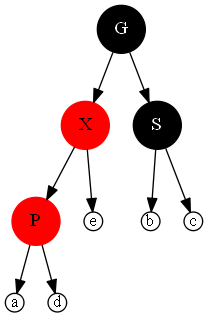

再对GX做一次右旋转并改变GX的颜色，SGI STL中提前改变了颜色，这是为了代码统一，不影响逻辑。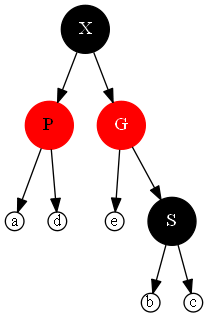

####情况3
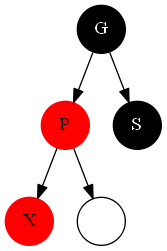
####情况4

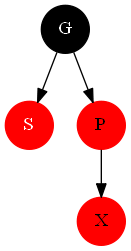
其实这种情况和情况1是相同的。

####情况5

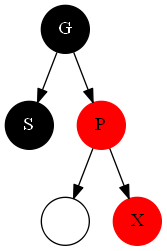
做一次左旋转

####情况6

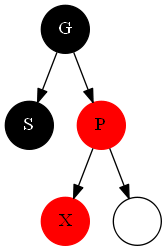
做一次右左双旋转

升序插入红黑树

降序插入红黑树

随机插入红黑树

###删除

删除红色节点

删除红色节点不影响红黑树的性质，可直接删除！

删除黑色节点

将右子节点的最左端节点代替该节点，然后进行reBlance。
如果后继节点为红色，则直接改成黑色，不需要reBlance。
经过节点A的所有路径长度都减少了1，reBlance过程中把这些情况分为以下4种。

节点A为删除后的替代节点，节点W为节点A的兄弟节点。

if (y->color != __rb_tree_red)
{   
    while (x != root && (x == 0 || x->color == __rb_tree_black))  
      if (x == x_parent->left)
      {  
        __rb_tree_node_base* w = x_parent->right;  
        //情况1  
        if (w->color == __rb_tree_red)
        {  
          w->color = __rb_tree_black;  
          x_parent->color = __rb_tree_red;  
          __rb_tree_rotate_left(x_parent, root);  
          w = x_parent->right;  
        }  
        //情况2  
        if ((w->left == 0 || w->left->color == __rb_tree_black) &&  
            (w->right == 0 || w->right->color == __rb_tree_black))
        {  
          w->color = __rb_tree_red;  
          x = x_parent;  
          x_parent = x_parent->parent;  
        }   
        else   
        {  
          //情况3  
          if (w->right == 0 || w->right->color == __rb_tree_black)
          {  
            if (w->left) w->left->color = __rb_tree_black;  
            w->color = __rb_tree_red;  
            __rb_tree_rotate_right(w, root);  
            w = x_parent->right;  
          }  
          //情况4  
          w->color = x_parent->color;  
          x_parent->color = __rb_tree_black;  
          if (w->right) w->right->color = __rb_tree_black;  
          __rb_tree_rotate_left(x_parent, root);  
          break;  
        }  
      }  
      if (x) x->color = __rb_tree_black;  
    }

####情况1

W为红色，AW的父节点为黑色。
对BD进行一次左旋，使得情况1转换成情况234中的一种。
####情况2

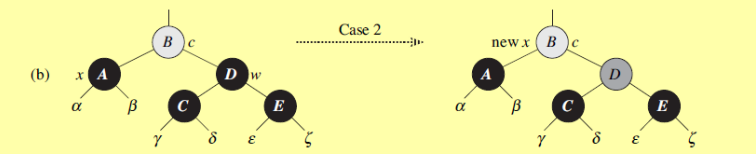
W和它两个子节点都为黑色
把W涂成红色，使得A和W两个子树路径长度都-1。
如果new x即B节点为红色，那么涂成黑色，就平衡了B节点的路径长。否则就需要上滤，继续平衡new x和其兄弟节点。
####情况3

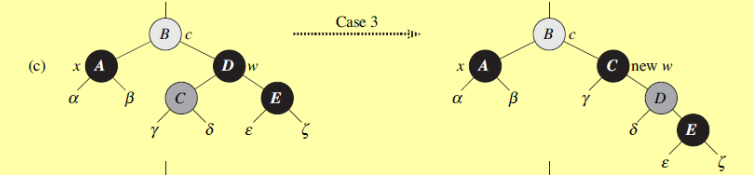
W为黑色，W的左节点为红色，右节点为黑色。
对WC进行一次右旋，转换为情况4
####情况4

W为黑色，右子节点为红色。
对BD进行左旋，并交换颜色，再把W的右节点置为黑色。

查找

while(x != 0)
    if(!key_compare(key(x), k))
        //x键值大于k
        y = x, x = left(x);
    else
        x = right(x);
iterator j = iterator(y);
//k的值比树中最大值都大，或者没有找到，则返回end()。  
//例如在root=10 10->left=8 10->right=14 14->left=11中查找12  
return (j == end() || key_compare(k, key(j.node())) ? end() : j;